突然想入门机器学习📖,把每周的内容记录到博客里,建立一个完整知识体系,也方便自己查阅。
笔者只是个非计算机专业👨💻的菜鸟,有理解的不够全面的内容,欢迎佬们交流赐教😍
笔者代码水平不高,大部分图片由draw.io绘制,如有错误,欢迎指正🥵
本篇内容创作时间已经超过了标题的一周,着实大鸽子
[1.1]📑引言(Foreword)
毫无疑问,人工智能是目前计算机科学中最热门的一个话题,机器学习是人工智能的一个分支,你如果能学会一些机器学习的技能,或许也能让机器🤖做很有趣的事情。
关于机器学习的定义有很多描述,而笔者更倾向于Tom M. Mitchell 👴的定义:
It’s a computer program learning from experience
Ewith respect to some taskTand some performance measureP, if its performance onTas measured byP, improves withE: Tom Mitchell 1998
机器学习存在几种不同类型的学习算法,主要的两种类型被我们称之为监督学习和无监督学习。
[1.2]📖监督学习(Supervised Learning)
监督学习是从标记🔖的训练数据来推断一个功能的机器学习任务。监督学习的目标是建立一个学习过程,将预测结果与“训练数据”(即输入数据)的实际结果进行比较,不断的调整预测模型,直到模型的预测结果达到一个预期的准确率,包括“回归(regression)”和“分类(classification)”等问题。

[1.2.1]回归(regression)
回归是对数值型连续随机变量进行预测和建模的监督学习算法。其特点是标注的数据集具有数值型的目标变量。
常用的回归方法包括:
- 线性回归:使用超平面拟合数据集
- 最近邻算法:通过搜寻最相似的训练样本来预测新样本的值
- 决策树和回归树:将数据集分割为不同分支而实现分层学习
- 集成方法:组合多个弱学习算法构造一种强学习算法,如随机森林(RF)和梯度提升树(GBM)等
- 深度学习:使用多层神经网络学习复杂模型
[1.2.2]分类(classification)
分类是一种对离散随机变量建模或预测的监督学习算法。分类通常基于回归方法扩展,适用于预测一个类别(或类别的概率)而不是连续数值。
常用的分类方法包括:
- 逻辑回归:对应线性回归方法,但使用了Sigmoid函数将预测映射为0到1之间的数值
- 分类树:对应回归树,又称为分类回归树(CART),将数据集分割为不同分支而实现分层分类
- 深度学习:使用多层神经网络分类
- 支持向量机(SVM):基于核函数计算支持向量之间的距离,并寻找最大化其与样本间隔的边界
- 朴素贝叶斯:基于贝叶斯定理和特征条件独立假设的分类方法
[1.2.3]两者的联系与区别
在回归问题中,我们采用一些评价方法比如SSE(sum of square errors)或拟合优度(Goodness of Fit),将一系列输入数据与实际数据比较,试图找到最优拟合,从而输出连续函数。
在分类问题中,我们则采用比如精度(accuracy)或混淆矩阵(error matrix)的评价方法, 试图寻找决策边界,将输入数据映射为离散数据。
对于我们判断研究的问题是分类问题还是回归问题,在不探究它们本质区别的情况下,我们最简单的判断方法就是看它的输出数据的类型,输出连续函数则对应回归问题,输出离散数据则对应分类问题。
举个🌰:
给你一年以来的某股票数据💹,预测一下明天股票的股价,股价作为时间的连续函数,因此这是回归问题,我们会尝试根据给定的数据去拟合出一个函数,从而推断明天的股价。
而改一下问题,还是给你一年以来的某股票数据,预测一下明天股票是跌📉还是涨📈,输出的跌涨情况是离散的数据,要么跌要么涨~~(不考虑持平)~~,那么很显然它转变为了分类问题,我们尝试寻找决策边界,推断出跌涨情况(或者其概率)。
[1.3]📕无监督学习(Unsupervised Learning)
根据没有被标记🔖的训练数据解决模式识别中的各种问题,称之为无监督学习。主要有聚类,异常检测,降维。无监督学习里典型例子是聚类,聚类的目的在于把相似的东西聚在一起,而我们并不关心这一类是什么。因此,一个聚类算法通常只需要知道如何计算相似度就可以开始工作了。[可以公开的情报]:小司🤩就是基于拆词和TextRank进行无监督学习群友们的话,事实上我也不知道它怎么学的那么多怪话🤡。
虽然所有数据未带标记,但是可以发现这些数据呈现出聚群的结构,本质是一个相似的类型的会聚集在一起。把这些没有标签🔖的数据分成一个一个组合,就是聚类(Clustering)。比如Google新闻,每天会搜集大量的新闻,然后把它们全部聚类,就会自动分成几十个不同的组(比如娱乐🎮,科技📡,生活🏠…),每个组内新闻都具有相似的内容结构。无监督学习是一种学习策略,交给算法大量的数据,并让算法为我们从数据中找出某种结构。
[1.4]📏单变量线性回归(Linear Regression with One Variable)
要明白单变量线性回归是什么,我们得先回忆[1.2.1]回归问题中,我们试图将输入数据拟合并输出连续函数。而如果输入数据和输出数据可以用线性关系近似表示,那么我们把它称为线性回归,只包括一个自变量和一个因变量的线性回归称为“单变量线性回归”。
[1.4.1]模型引入
我们观察这样一组数据:

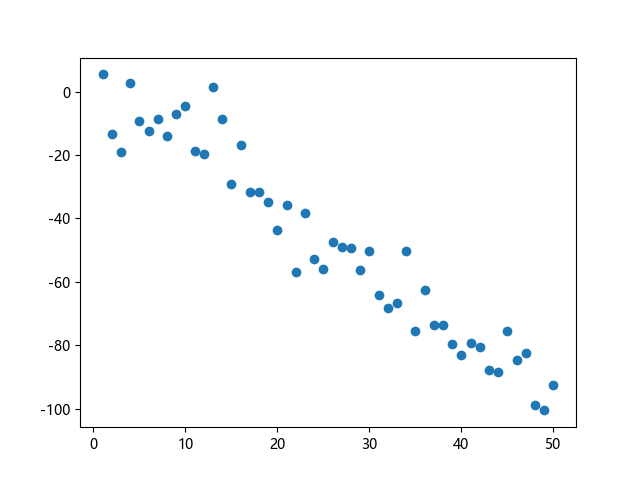
在我们看来,这些输入数据在某种程度上好像有相似的地方,比如 随 的增大呈现出一种线性递增📈或者线性递减📉的趋势。那我们想定量的去衡量这种线性的递增递减关系,就会想到能不能找到一个线性函数来尽可能的接近这些数据,用这个线性函数来预测或者是描述之后的输入数据。
✨你也可以通过笔者写的这样一段代码生成上面的图像:
import matplotlib.pyplot as plt import numpy as np n = 50 # 数据个数 x = np.linspace(1, n, n).reshape(-1, 1) y = np.random.choice([-2,-1,1,2]) * x y += np.random.randn(n, 1) * 10 plt.figure() plt.scatter(x,y) plt.show()
[1.4.2]模型函数
我们将要用来描述这个回归问题的标记🔖如下:
代表训练集中实例的数量
代表特征(feature)
代表目标值(target)
代表预测值(prediction)
代表训练集中的实例
代表第个观察实例
根据[1.4.1],我们假设这样一个模型函数:
显然有 ,于是我们接下来就要找到一种评价方法来定量描述这个模型函数与输入数据之间的接近程度。
[1.4.3]代价函数/损失函数(cost Function)
要想准确的衡量我们模型函数的好坏,我们得要选取一个代价函数来定量描述预测值和目标值的的差异程度。在线性回归问题中,一般采用最小二乘估计,代价函数为残差平方和(SSE,Sum of Squares for Error)
但如果对于不同数据量的样本,样本数少就意味着参与求和的数据少,对应的 也会相应变小,但这不是我们希望看到的,我们不希望样本量影响代价函数的大小。所以我们对它求平均值,我们采用的代价函数是均方误差(MSE,Mean squared error)
其实除以 或 代价函数最优化的结果都是相同的,这里为了后续求导计算方便,因此用 处理。
为什么这个代价函数能够衡量预测值和目标值之间的差异呢?我们观察下面这组图(由draw.io绘制):
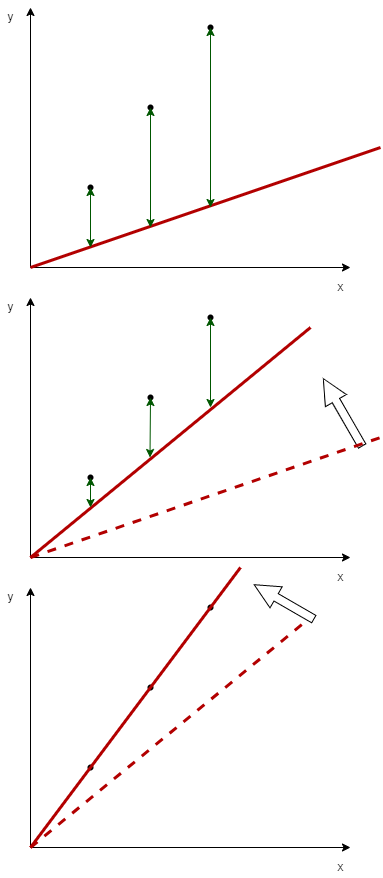
假如我想要拟合左图中的 3 个点,对于 ,我们令 ,那么我们尝试把直线 从 开始旋转🔄 (图1->图二->图三),而绿色的线段长度 则表示预测值和目标值之间的距离,可以发现绿色的线段长度随着直线的旋转逐渐减小,而代价函数 也随之减小。很显然,我们发现图三的拟合效果最好,此时的代价函数 ,我们找到了最佳拟合的模型函数。
如果有两个参数 和 ,那么它们的代价函数 则是一个三维的图像:

我们用draw.io绘制一张等高线图,则可以看出在三维空间中存在一个使得 最小的点:
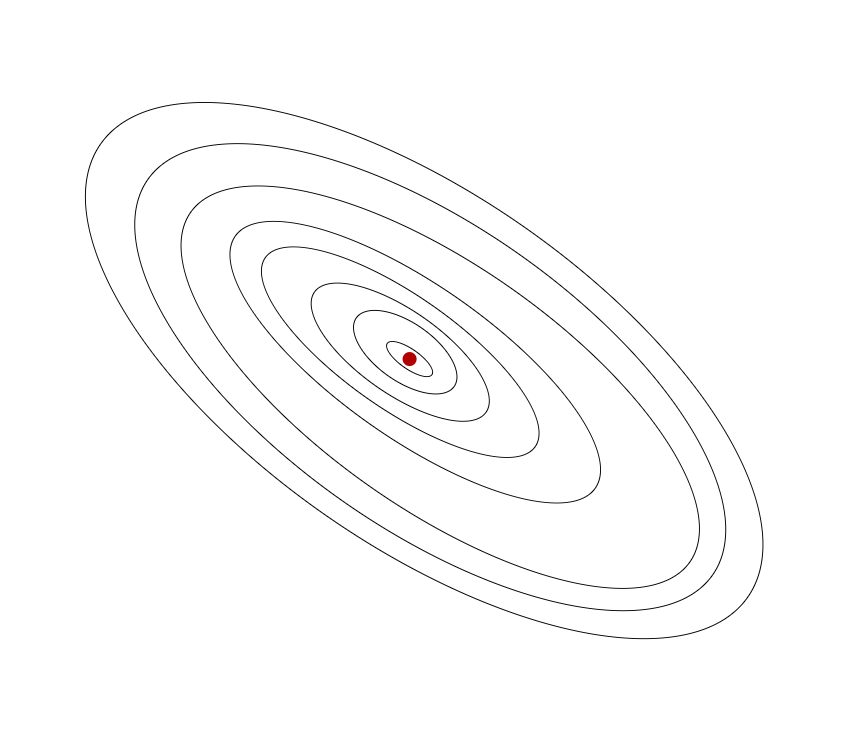
当然,我们也不希望编个程序把这些点画出来,然后人工的方法来读出这些点的数值,这很明显不是一个好办法 😵(也太不智能了)。我们会遇到更复杂、更高维度、更多参数的情况,而这些情况是很难画出图的,因此更无法将其可视化。我们真正需要的是一种有效的算法,能够自动地找出这些使代价函数 取最小值的参数 和 。
[1.4.3]梯度下降法(Gradient descent)
你可能需要一些高等数学📚的知识(梯度相关概念)
模型收敛过程:
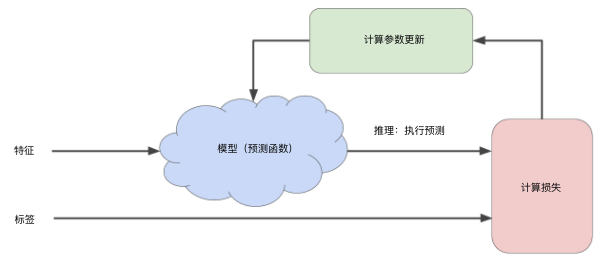
梯度下降是机器学习中最常用的计算代价函数的方法,它只需要计算代价函数的一阶导数,我们将使用梯度下降算法来求出代价函数 的最小值。
梯度下降背后的思想是:开始时我们随机选择一个参数的组合 ,计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值(local minimum)。
举个🌰:
想象一下你正站立在山顶🗻上,想要尽快下山,在梯度下降算法中,你要做的就是看看周围,判断哪个下山的方向最陡,然后向着那个方向跨出一段步长,到达新的一个位置。此时你站定,继续看看周围那个下山的方向最陡,并向着那个方向跨出一段步长。重复上面的步骤,你会发现自己下到了山的最底部。

我们先从简单的单个参数开始研究,对于单个参数 ,我们根据其梯度负方向来更新 ,梯度下降算法用以下伪代码表示:
(其中是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。)
对于单个参数,导数就等于梯度值,而导数的值又等于切线的斜率。现在看到下面那张图,在点 画一条切线,很明显斜率 为负,也就是对应的导数和梯度值都为负数。根据梯度下降算法 ,我们得到的新 其中 ,则 向右移动一段距离,更加靠近最低点,这正是我们所希望的。而当移动到局部最优点时,该点的导数等于零,接下来 将不再改变,代价函数收敛到局部最低点。
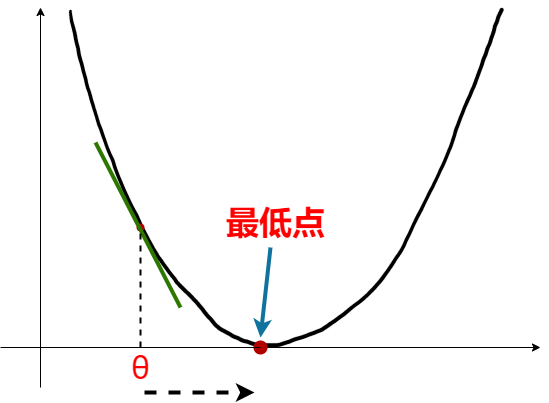
💦值得注意的是,对于学习率 :
如果 太小了,即我的学习速率太小,结果就是只能这样像小宝宝👶一样一点点地挪动,去努力接近最低点,这样就需要很多步才能到达最低点,所以如果 太小的话,可能会很慢,因为它会一点点挪动,它会需要很多步才能到达全局最低点。
如果 太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛,下一次迭代又移动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来越远,所以,如果 太大,它会导致无法收敛,甚至发散。
接下来,我们回到线性回归问题,梯度下降用以下伪代码表示:
我们刚刚使用的算法,有时也称为批量梯度下降。实际上,在机器学习中,通常不太会给算法起名字,"批量梯度下降"指的是在梯度下降的每一步中,我们都用到了所有个训练样本。而事实上,有时也有其他类型的梯度下降法,不是这种"批量"型的,不考虑整个的训练集,而是每次只关注训练集中的一些小的子集(mini-batch梯度下降或者随机梯度下降)。
如果你之前学过线性代数📚,你应该知道有一种计算代价函数 最小值的数值解法,不需要梯度下降这种迭代算法。在后面的学习中,我们也会谈到这个方法,它可以在不需要多步梯度下降的情况下,也能解出代价函数 的最小值,这是另一种称为正规方程(normal equations)的方法。实际上在数据量较大的情况下,梯度下降法比正规方程要更适用一些。
现在我们已经掌握了梯度下降,我们可以在不同的机器学习问题中大量地使用它。或许你之前没接触过机器学习的相关内容,🎉🥳祝贺你成功学会你的第一个机器学习算法。
[1.4.4]线性回归的梯度下降算法的代码实现(Gradient Descent For Linear Regression)
到现在,我们已经学过了单变量线性回归的模型函数、代价函数和梯度下降法,我们可以尝试用Python🐍简单实现一个完整的单变量线性回归:
(🥰希望你通过以下这段代码,也能自己实现一个单变量线性回归)
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
n = 20 # 数据个数
x = np.linspace(1, n, n).reshape(-1, 1)
y = np.random.randint(-5, 5, size=1) * x + np.random.randint(-5, 5, size=1)
y += np.random.randn(n, 1) * 2
alpha = 0.01 # 学习率
w = 0
b = 0
# 均方误差函数
def cost_func(x, y, w, b):
cost = 0
for i in range(n):
fwb = w * x[i] + b
cost += (fwb - y[i]) ** 2
cost = 0.5 * cost / n
return cost
# 梯度计算
def gradient(x, y, w, b):
dw = 0
db = 0
for i in range(n):
fwb = w * x[i] + b
dy = fwb - y[i]
db += dy
dw += dy * x[i]
dw = dw / n
db = db / n
return dw, db
# 梯度下降法
def gra_descent(x, y, w, b, alpha):
dw, db = gradient(x, y, w, b)
i = 0
lossList = []
while True:
dw, db = gradient(x, y, w, b)
w -= alpha * dw
b -= alpha * db
if (abs(dw) < 1e-5) and (abs(db) < 1e-5):
break
if i < 10000:
lossList.append(cost_func(x, y, w, b))
i = i + 1
else:
break
print(f"(the total number of iterations is {i} times)")
return w, b, i, lossList
fig, ax = plt.subplots(1, 2, constrained_layout=True, figsize=(12, 4))
# 线性回归图
x1 = np.arange(0, n + 1, n / 5)
w1, b1, i, lossList = gra_descent(x, y, w, b, alpha)
fwb1 = w1 * x1 + b1
ax[0].scatter(x, y)
ax[0].set_title('Gradient Descent For Linear Regression')
ax[0].plot(x1, fwb1, label=f"y = {'%.3f' % w1}x+{'%.3f' % b1} ", c='r')
ax[0].legend()
# 学习曲线
x2 = np.arange(150)
ax[1].set_title(f'Loss function curve (the total number of iterations is {i} times)')
ax[1].plot(x2, lossList[:150], c='b')
plt.show()或许你会得到和以下这张图类似的图像,我们可以清楚的看到,左图直线拟合得很令我们满意,右图损失函数也收敛于0附近。
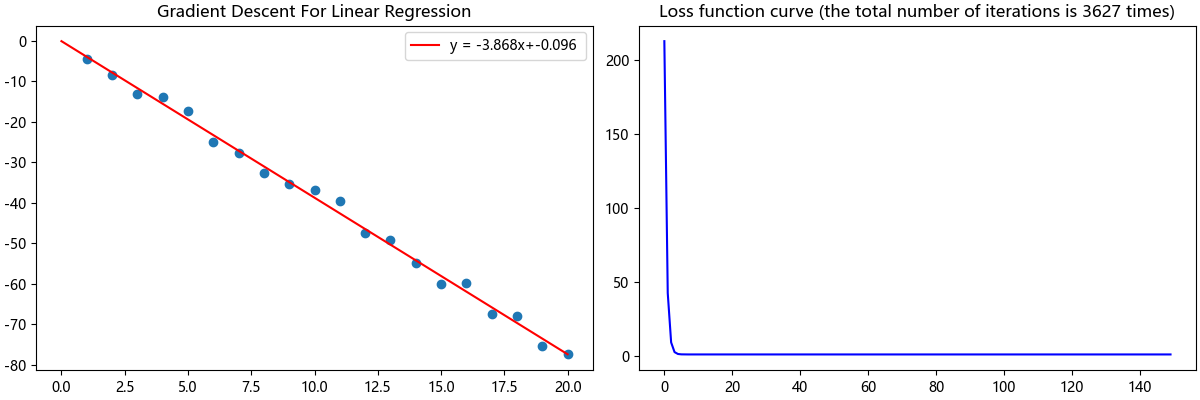
如果你尝试运行了以上的代码,你就会发现,再增大数据量n就会导致溢出😖,运行速度也减慢。这是因为我们没有对数据进行标准化和归一化处理,当然,这不是我们现在要探究的内容。如果你通过阅读笔者上面的Python代码,自己也实现了一个单变量线性回归,那么🎉🥳祝贺你从算法底层理解并实现了单变量线性回归。
在实际开发过程中,我们或许会直接使用TensorFlow或pytorch直接运行单变量线性回归的模型进行数据的拟合,以下是使用Python的TensorFlow库实现单变量线性回归的代码:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# 参数初始化
n = 101 # 数据个数
m = 0.5 # 数据离散程度
k = np.random.choice([-2, -1, 1, 2]) # 近似的斜率
# 数据生成
x = np.linspace(-1, 1, n).reshape(-1, 1)
y = k * x + np.random.randn(n, 1) * m + 3
x = x.astype(np.float32)
y = y.astype(np.float32)
# 转为tensor
X = tf.constant(x)
Y = tf.constant(y)
w = tf.Variable(tf.zeros([1]))
b = tf.Variable(tf.zeros([1]))
variable = [w, b]
# 优化器
optimizer = tf.keras.optimizers.SGD(learning_rate=0.001) # 这里使用的是随机梯度下降
def linear_regression(w, b, X, Y, epoch=500):
lossList = [] # 损失函数
for i in range(epoch):
with tf.GradientTape() as tape:
Y_hat = w * X + b
loss = tf.reduce_sum(tf.square(Y_hat - Y))
lossList.append(loss)
grad = tape.gradient(loss, variable)
optimizer.apply_gradients(grads_and_vars=zip(grad, variable))
lossList = [loss.numpy() for loss in lossList]
w = w.numpy()
b = b.numpy()
return lossList, w, b
lossList, w, b = linear_regression(w, b, X, Y)
fig, ax = plt.subplots(1, 2, constrained_layout=True, figsize=(12, 4))
# 线性回归图
x1 = np.arange(-1, 1, 0.05)
fwb1 = w * x1 + b
ax[0].scatter(x, y)
ax[0].set_title('grd')
ax[0].plot(x1, fwb1, label=f"y = {'%.3f' % w}x+{'%.3f' % b} ", c='r')
ax[0].legend()
# 学习曲线
x2 = np.arange(len(lossList))
ax[1].set_title('loss')
ax[1].plot(x2, lossList, c='b')
plt.show()或许你会得到和以下这张图类似的图像,细心的你可能会发现输入数据量和第一段代码相比增加了很多,这是因为我们在生成数据时进行了归一化处理,并且我们使用的梯度下降算法是随机梯度下降(SGD),通过这样一些操作我们可以拟合更大量的数据:
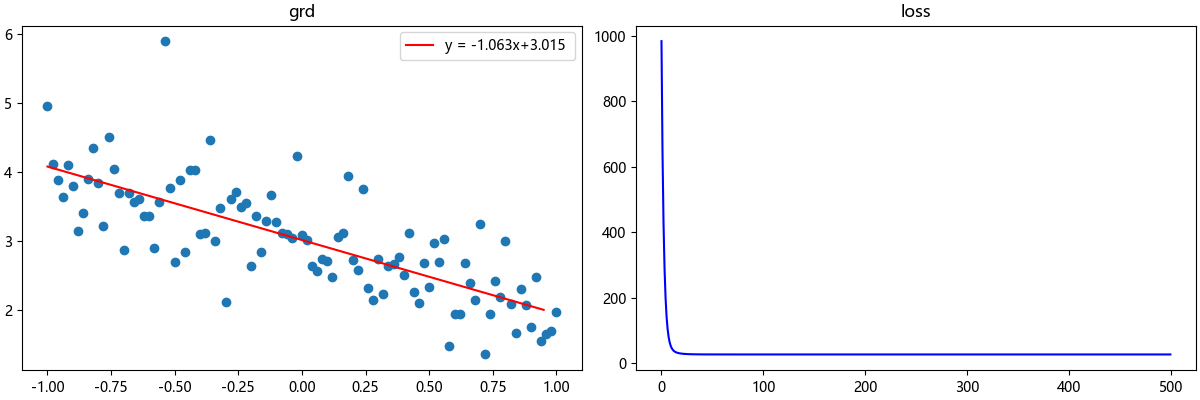
💞当然,笔者希望你能理解在线性回归当中梯度下降和代价函数是怎么工作的,而不是直接引用TensorFlow库的一些封装好的函数。理解这些算法是怎么运作的,对我们实际开发和调试会有更大的帮助。
本周我们简单了解了机器学习和两大学习方式的概念,掌握了第一个深度学习算法————梯度下降法,学习了如何实现线性回归,并通过代码实战理解了它们的算法实现。
(如果喜欢本文章,求求来个评论来个反应吧🥺🥺🥺)


